Precept
The core concept behind bodily RC is designing and using a dynamic system as a reservoir to map enter information into larger dimensions40. Latest researches reveal that NG-RC can surpass standard RC by requiring far fewer metaparameters to optimize, shorter coaching datasets, and considerably fewer node dimensions in comparison with comparable reservoir computer systems41. The precept of the NC-RG is proven in Fig. 1b. The NG-RC features comparable to traditional RC, but it surely doesn’t require constructing a fancy recurrent NN with nonlinear nodes. As a substitute, it operates as a feedforward community, the place the nodes signify totally different types of transformations of the enter (known as a characteristic vector). The output is then a linear regression of those components within the characteristic vector (see Fig. 1b). Mathematically, such a characteristic vector may be expressed as:
$${{{bf{O}}}}_{{rm{complete}}}=coplus {{{bf{O}}}}_{{rm{linear}}} oplus {{{bf{O}}}}_{{rm{nonlinear}}}$$
(1)
the place ⊕ represents the vector concatenation operation, c is a continuing, Olinear is the linear vector ({{bf{X}}}={[{x}_{t},{x}_{t-1},…,{x}_{t-(N-1)}]}^{T}), and Ononlinear is the nonlinear transformation of the inputs. Whereas it’s versatile to pick the nonlinear transformations, a easy quadratic polynomial of the inputs has been demonstrated to have good computing capabilities35. Due to this fact the nonlinear characteristic Ononlinear is given by:
$${{{bf{O}}}}_{{rm{nonlinear}}}={{{bf{O}}}}_{{rm{linear}}}otimes {{{bf{O}}}}_{{rm{linear}}}$$
(2)
the place ⊗ represents the outer product operation. It’s value noting that within the NG-RC, the dimension of the output vector Ocomplete is considerably smaller than that in comparable RC methods35. When the enter vector accommodates a sign of the size of N and a relentless, the scale of the Ocomplete solely must be (frac{(N+1)(N+2)}{2}), which features a fixed c, N inputs, and (frac{N(N+1)}{2}) quadratic polynomials of inputs. The consequence yout is the linear mixtures of the weather in Ocomplete with weights skilled by linear regression.
Single wavelength operation: Fig. 1c, d illustrate our proposed photonic RC chip guided by the NG-RC framework. The enter information X is encoded onto the amplitude of a laser with a wavelength of λ. The enter is then cut up into N delayed copies despatched right into a star coupler along with an unmodulated laser representing the fixed c. The neighboring delay line introduces a time delay of Δt, which is the same as one image period of the enter sign. These delay strains make sure that enter information at totally different instances concurrently attain the adopted star coupler. After the star coupler, the output vector ystar,λ is expressed as:
$${{{bf{y}}}}_{star,lambda }={{{boldsymbol{omega }}}}_{star,lambda }cdot (coplus {{bf{X}}})$$
(3)
Right here, ωstar,λ denotes an M × (N + 1) complicated matrix, representing the switch perform of the star coupler at wavelength λ, the place N is the variety of delayed enter copies and M is the variety of outputs of the star coupler.
The outputs from the star coupler are adopted by a readout layer, which may be carried out both digitally or optically. In a digital implementation, every output of the star coupler is detected by a photodetector, producing an output given by:
$$start{array}{rcl} y_{P D,i} &=& left|{{boldsymbol{omega}}}_{star,lambda,i} cdot(c oplus {{mathbf{X}}})proper|^2 hfill &=& underbrace{c_{i}}_{{{rm{fixed }}}}+underbrace{sumlimits_{n=1}^{N} a_{n,i} x_{t+1-n}}_{{{rm{linear}}},{{rm{phrases}}}}+underbrace{sumlimits_{m=1}^{N} sumlimits_{n=m}^{N} b_{mn,i} x_{t+1-m} x_{t+1-n}}_{{{rm{quadratic}}},{{rm{phrases}}}} finish{array}$$
(4)
the place yPD,i is the output of the photodetector and ci, an,i, and bmn,i are constants, that are decided by the switch perform of the star coupler. Eq. (4) exhibits that the output of every photodetector is a mix of fixed, linear inputs, and their quadratic polynomials. M outputs kind a vector yPD, the place every component is the same combination however with totally different coefficients decided by the switch perform matrix of the star coupler. When the variety of outputs (Mge frac{(N+1)(N+2)}{2}), yPD may be reworked into the characteristic vector required by the NG-RC, consisting of fixed, linear, and nonlinear elements, utilizing a linear matrix. On this case, the system features equivalently to the NG-RC. It’s value noting that the precise values within the switch perform of the star coupler don’t have an effect on the ultimate computing consequence as a result of the readout layer after the star coupler may be skilled and adjusted to make sure optimum values. This characteristic makes our system have a excessive tolerance for fabrication errors.
To comprehend an optical readout layer, one strategy is to cross the outputs from the star coupler by way of an array of programmable microring resonators (MRRs)(the primary column of MRRs in Fig. 1c). The resonance wavelengths of the MRRs are aligned with the enter wavelength. By adjusting the resonance of every MRR utilizing an embedded thermal section shifter, the fraction of sunshine directed to the Drop ports may be finely managed. Along with tuning the sign’s amplitude through the section shifter on the MRR, a second section shifter on the bus waveguide adjusts the sign section. The mixed tuning of those two section shifters allows exact management of complicated weights. The weighted alerts are then detected by a balanced photodetector (BPD). The outputs from the primary (frac{M}{2}) rows of MRRs are mixed and detected by one photodiode, whereas the remaining MRR outputs are mixed and detected by a second photodiode. The differential sign between the 2 photodiodes offers the total vary of weights, together with constructive and destructive values. The ultimate sign after the BPD is given by:
$$start{array}{rcl} y_{B P D,lambda} &=& left|{{boldsymbol{omega}}}_{{{mathrm{MRR}}}}^{+} {{mathbf{y}}}_{{{rm{star}}},lambda}^{+}proper|^2-left|{{boldsymbol{omega}}}_{{{mathrm{MRR}}}}^{-} {{mathbf{y}}}_{{{rm{star}}},lambda}^{-}proper|^2 hfill &=& underbrace{c}_{{{rm{fixed}}}}+underbrace{sumlimits_{n=1}^{N} omega_{{{mathrm{lin}}},n} x_{t+1-n}}_{{{rm{linear}}},{{rm{phrases}}}}+underbrace{sumlimits_{m=1}^{N} sumlimits_{n=m}^{N} omega_{{{rm{nonlinear}}},m n} x_{t+1-m} x_{t+1-n}}_{{{rm{quadratic}}},{{rm{phrases}}}} finish{array}$$
(5)
the place ({{{boldsymbol{omega }}}}_{{{rm{MRR}}}}^{+}) and ({{{boldsymbol{omega }}}}_{{{rm{MRR}}}}^{-}) are complicated weight vectors given by the primary and second half rows of MRRs, respectively. ({{{bf{y}}}}_{star,lambda }^{+}) and ({{{bf{y}}}}_{star,lambda }^{-}) are the output vectors from the primary (frac{M}{2}) outputs and second (frac{M}{2}) outputs of the star coupler, respectively, given by Eq. (3). Eq. (5) signifies that the output of the BPD is a regression of the fixed, inputs, and quadratic polynomials of inputs. The regression coefficients c, ωlin, and ωnonlinear may be programmed from -1 to 1 utilizing the MRR array. Due to this fact, the outputs of the optical engine have an equal perform to these of the NG-RC. The derivation particulars of Eq. (5) are supplied within the Supplementary Observe 3.
For a given enter port measurement N + 1 pushed by N delayed enter copies and one fixed, the computing efficiency improves because the variety of outputs M of the star coupler will increase, and this efficiency reaches saturation when (M=frac{(N+1)(N+2)}{2}). Rising the computing efficiency requires a really slight improve within the measurement of the star coupler to accommodate extra enter and output waveguides, with out altering its design. We estimate {that a} star coupler with an space of 6.25 mm2 can assist greater than 5000 outputs, and this quantity is proscribed by the optical energy to make sure an affordable signal-to-noise ratio (SNR) (See evaluation particulars within the Dialogue and Supplementary Observe 7).
Scaling to multi-wavelength operation: Along with rising the variety of outputs M, the computing functionality may be additional scaled up by way of wavelength-division multiplexing (WDM). As proven in Fig. 1c, d, the enter information X is encoded onto an array of WDM lasers with P distinct wavelengths. On the output of the star coupler, the alerts at totally different wavelengths are individually weighted by a column of MRRs. Every column is designed with a definite resonance wavelength, aligned with the corresponding WDM laser, permitting exact management and weighting of the optical alerts throughout a number of wavelengths. After the BPD, the output is the summation of the photoelectric currents generated by totally different wavelengths, which is given by ({y}_{BPD}={sum }_{i=1}^{P}{y}_{BPD,lambda i}). Using WDM additional will increase the dimension of the output vector from M to M × P.
Machine design and experimental setup
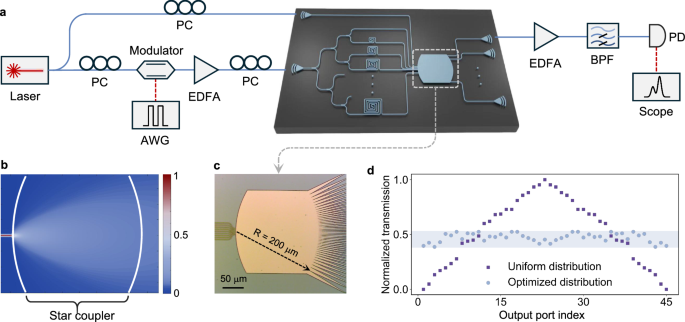
Determine 2a exhibits the photonic chip utilized in our experiment, constructed on a silicon-on-insulator (SOI) platform. In accordance with the final idea of common approximations, the enter measurement is ideally thought of to be infinitely giant42. Nevertheless, empirical remark means that the Volterra collection converges shortly, even with a comparatively small enter dimension35. Consequently, the variety of delay strains doesn’t should be giant. In our demonstration, our system makes use of 8 delay strains with incremental lengths to supply 8 delayed copies of the enter sign, leading to a compact photonic RC system. The sign is evenly divided into eight copies by on-chip splitters. Every copy experiences a special delay brought on by an array of delay strains with incremental delay. The incremental delay is ready at 16.7 ps (akin to 1.18 mm of silicon waveguide) to accommodate a 60 GBaud enter sign. The star coupler occupies a footprint of 0.04 mm2, with 9 inputs (one for unmodulated mild and eight for delayed sign copies) and 45 (i.e., (9 + 1) × 9/2) outputs to generate the mandatory characteristic vector. As mentioned within the Precept part, mathematically, any full-rank transmission matrix from the star coupler would suffice. Nevertheless, contemplating a decrease energy density on the edges in comparison with the middle, we design the widths of the output ports to lower quadratically from the sting to the middle, as proven in Fig. 2c. This optimized design ensures that every output maintains an almost uniform energy distribution and SNR throughout all ports, as proven in Fig. 2d. The sunshine transmission throughout the star coupler is simulated utilizing Finite-Distinction Time-Area (FDTD) and proven in Fig. 2b. The star coupler along with delay strains features equivalently to the enter and reservoir layer in standard RC methods however with a footprint of solely 2 mm2, considerably smaller than the reservoir layer in different RC methods. Methodology offers chip design and fabrication particulars.
a Experimental setup with the fabricated system. PC, polarization controller. AWG, arbitrary waveform generator. EDFA, erbium-doped fiber amplifier. BPF, bandpass filter. PD, photodiode. b FDTD simulation results of mild transmission within the star coupler. c Microscope picture of the optimized star coupler. The diameter of the star coupler is 200 μm. d The normalized transmission of every output port when the width distribution of output ports is uniform or optimized.
The experimental setup is illustrated in Fig. 2a. We first exhibit the operation of our NG-RC chip utilizing a single wavelength, and lengthen the demonstration to a number of wavelengths within the later part. For the single-wavelength demonstration, we use a continuous-wave laser working at 1550 nm as our mild supply. The sunshine is cut up into two equal branches by a 50/50 coupler. One department is coupled to the photonic chip as a relentless reference c, whereas the opposite is modulated by a thin-film lithium niobate depth modulator (LIOBATE, LB4C6PSBM63, 40 GHz bandwidth, RF Vπ ≈ 3 V). The enter sign, generated by an arbitrary waveform generator (AWG, KEYSIGHT, M8199A, 256 GSa/s), is encoded onto the amplitude of the sunshine by the modulator. To attain a 60 Gbaud line price, we set the pattern price of the AWG to 240 GSa/s. The modulator is configured in a push-pull association and biased on the null level, akin to the minimal mild depth. The voltage utilized to the modulator is ready to ∣V∣ Vπ/4 guaranteeing that the enter information may be linearly modulated onto the laser’s amplitude. The modulated mild is then amplified by an erbium-doped fiber amplifier (EDFA) earlier than being injected into the photonic chip. In our experiment, the readout layer of the NG-RC is carried out digitally. The optical outputs are coupled out and detected sequentially utilizing an off-the-shelf photodetector (COHERENT, mannequin XPDV3120R-VM-FA, with a 70 GHz bandwidth) and digitized by a real-time oscilloscope (KEYSIGHT, mannequin UXR0592AP, with a 59 GHz bandwidth and 256 GSa/s sampling price). Lastly, the readout layer is skilled utilizing a digital pc. As mentioned within the Precept part, the readout layer will also be carried out optically and in real-time.
Duties for sequence prediction
We first consider the efficiency of our photonic NG-RC chip on sequence prediction by way of two benchmark duties: the Santa Fe Laser dataset and the Lorenz63 system. In a prediction process, the aim is to foretell the long run output of a dynamical system primarily based on the previous output43. Prediction duties may be categorized into two classes: (i) when the system dynamics are unknown, and (ii) when the system dynamics are recognized.
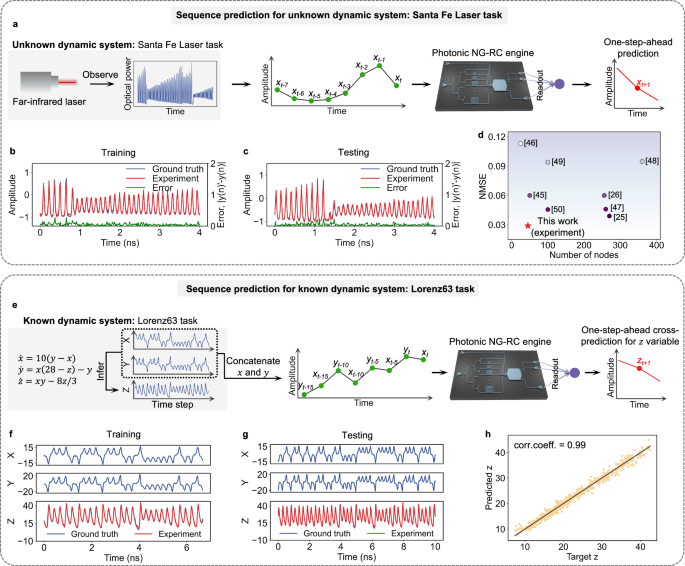
The Santa Fe Laser dataset is generated from a chaotic system with unknown dynamics, consisting of experimental measurements of the optical energy emitted by a laser working in a chaotic regime44. On this process, the goal is to coach the photonic NG-RC chip to foretell the subsequent sampling level xt+1 generated from the laser primarily based on the earlier sampling factors, as proven in Fig. 3a. We use 6000 sampling factors to coach the readout layer, aiming to search out the optimum set of 45 weights on the readout layer that fulfill xt+1 = woutyPD utilizing Tikhonov regularization. 2500 factors are used for testing. Determine 3b, c present the anticipated sequences from our photonic NG-RC system in the course of the coaching and testing phases, each of which carefully align with the goal sequences. The prediction accuracy is assessed utilizing the Normalized Imply Sq. Error (NMSE), outlined as (NMSE=frac{{sum }_{n}{left[{x}^{{prime} }(n)-x(n)right]}^{2}}{{sum }_{n}{left{x(n)-frac{{sum }_{n}[x(n)]}{n}proper}}^{2}}), the place ({x}^{{prime} }(n)) and x(n) signify the anticipated and goal sequence, respectively. The NMSE generated by our system is 0.029. In Fig. 3d, we evaluate the efficiency of our system with beforehand reported work25,26,45,46,47,48,49,50 by displaying their readout layer dimensions and the achieved NMSE. The outcomes present that our photonic NG-RC system achieves the bottom NMSE with the smallest output dimension, whereas additionally demonstrating the quickest processing pace in comparison with the opposite methods.
a Workflow for performing Santa Fe Laser process utilizing our photonic NG-RC chip. b The expected sequence (pink) and goal sequence (blue) for the Santa Fe laser process throughout coaching. c The expected sequence (pink) and goal sequence (blue) for the Santa Fe laser process throughout testing. d Efficiency comparability on the Santa Fe Laser process with different reported work, specializing in NMSE versus the variety of nodes. e Workflow for predicting the z variable utilizing the x and y variables from the Lorenz63 system. The Lorenz63 is a recognized dynamic system. f Floor reality (blue) and prediction (pink) variables of Lorenz63 in the course of the coaching section. X, and Y variables are fed into photonic NG-RC system, and the Z variable is predicted. g Floor reality (blue) and predicted (pink) variables of Lorenz63 in the course of the testing section. h Correlation between predicted z and goal z. The correlation coefficient, primarily based on testing 600 information factors, exceeds 0.99.
We then exhibit the effectiveness of our NG-RC chip utilizing a Lorenz63 time collection forecasting process. Lorenz63 dataset is generated from a chaotic system the place the system dynamics are recognized and may be described by a set of three coupled abnormal differential equations51:
$$dot{x}=10(y-x),dot{y}=x(28-z)-y,dot{z}=xy-8z/3$$
(6)
The Lorenz63 system serves as a paradigmatic instance of deterministic chaos. On this process, the aim is to foretell the subsequent worth of z one step forward utilizing the present values of x and y. This cross-prediction process is totally different and more difficult in comparison with most photonic reservoir computing demonstrations, which generally predict future x, y, z values from previous x, y, z values52,53. This process holds sensible significance, because it showcases the potential to make use of observable sensory information to deduce unobservable data.
Determine 3e exhibits the workflow of our photonic NG-RC system for dealing with the Lorenz63 process. To generate the coaching and testing dataset, we resolve Eq. (6) utilizing a time step of 0.05. We use 400 information factors for every variable x, y, z for coaching and 600 information factors for every variable for testing. The detailed information processing technique for the Lorenz63 process is supplied in Methodology. Determine 3f, g present the anticipated z sequence in the course of the coaching and testing section, which carefully matches the bottom reality. The correlation between the anticipated and goal z values, primarily based on 600 take a look at information factors, exceeds 0.99, as proven in Fig. 3h. The experimental NMSE for the Lorenz63 process is 1.43 × 10−2 utilizing solely 45 output nodes. This NMSE may be additional diminished by using a modulator with a better bandwidth (at the moment, a 40 GHz modulator generates a 60 Gbaud sign). In digital simulations, with out bandwidth constraints, the NMSE may be diminished to three × 10−4 with 45 nodes. As compared, ref. 37 studies an NMSE of 0.9 × 10−2 utilizing over 2000 nodes.
Duties for system emulation
We additional consider the power of our photonic NG-RC chip for system approximation and emulation. In a system emulation process, the RC system is skilled to approximate the response of a dynamical system43. Such approximations may be categorized into two varieties, relying on whether or not the system dynamics are recognized or unknown. This process has sensible functions in sign processing. Right here, we exhibit two duties.
The primary process is nonlinear channel equalization (NCE), which goals to recuperate the unique sign from the noisy sign distorted by a nonlinear multipath RF channel. After profitable coaching, our photonic NG-RC chip may be handled as an unknown nonlinear filter able to eradicating the nonlinear noise on this system. The symbols of the unique sign d(n) are randomly chosen from the set { − 3, − 1, 1, 3}. The distorted sign u(n) is outlined as
$$q(n)= 0.08d(n+2)-0.12d(n+1)+d(n)+0.18d(n-1)-0.1d(n-2) +0.091d(n-3) -0.05d(n-4)+0.04d(n-5)+0.03d(n-6) +0.01d(n-7)$$
(7)
$$u(n)=q(n)+0.026q{(n)}^{2}-0.011q{(n)}^{3}$$
(8)
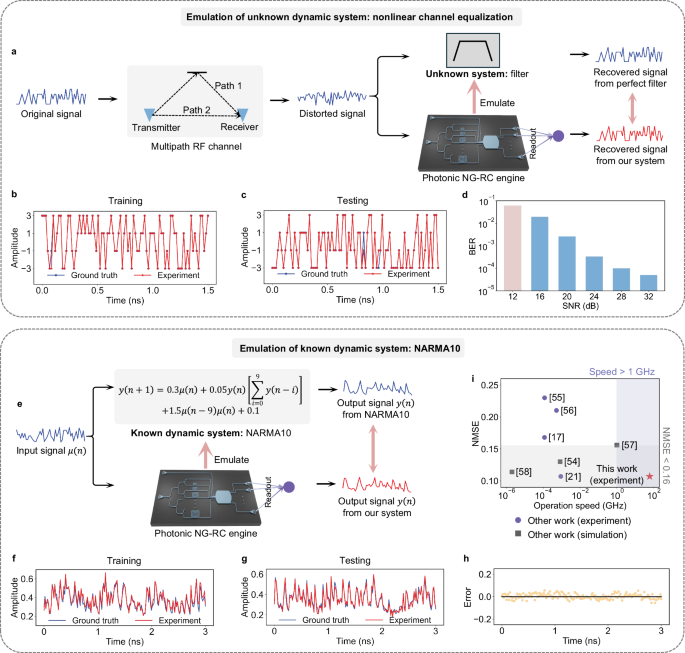
Determine 4a exhibits the workflow of emulating the right filter utilizing our photonic NG-RC chip. Within the NCE process, we use 3000 information factors for coaching and 6000 for testing. The recovered waveforms from the coaching and testing phases are proven in Fig. 4b and c, respectively. Throughout the coaching section, the recovered sign carefully matches the unique sign. Within the testing section, minor errors are noticed, leading to a bit error price (BER) of 0.06. This BER is measured at an experimental SNR of 12 dB. The comparatively low SNR is as a result of bandwidth limitations of the modulator. The experimental BER is decrease than these reported in refs. 17,21,46,54 when the SNR is 12 dB. We additional simulate the BERs when the SNR improves as proven in Fig. 4d. If a better bandwidth modulator is used, the BER may be diminished to beneath 10−4.
a Idea of emulating an unknown filter utilizing our photonic NG-RC system. b, c Experimental outcomes in the course of the coaching (b) and testing (c) phases within the NCE process. The reconstructed sign (pink) and the unique sign (blue) are plotted. d The experimental consequence exhibits a BER of 0.06 at an SNR of 12 dB, together with the simulated BER for various SNR ranges. e Idea of emulation of a recognized dynamic system (NARMA10) with our photonic NG-RC system. f, g Experimental outcomes in the course of the coaching (f) and testing (g) phases within the NARMA10 process. The generated sequence (pink) and the goal sequence (blue) within the NARMA10 process are plotted. h The error between the experimental outcomes and floor reality in the course of the testing section. i Comparability of the efficiency on the NARMA10 process with different reported work, specializing in NMSE versus the operation pace.
The second system emulation process we carry out is the Nonlinear Auto-Regressive Shifting Common (NARMA10) process, which is without doubt one of the most-used benchmark duties within the subject of reservoir computing. The target is to coach our photonic NG-RC chip to copy the conduct of a Tenth-order nonlinear system, which has recognized dynamics modeled by the next recurrent equation:
$$y(n+1)=0.3mu (n)+0.05y(n)left[mathop{sum }_{i=0}^{9}y(n-i)right]+1.5mu (n-9)mu (n)+0.1$$
(9)
the place μ(n) is the system enter, sampled from a uniform distribution inside [0, 0.5], and y(n) is the system output. We practice our system to generate the output y(n + 1) primarily based on enter μ(n). Determine 4e exhibits the workflow for emulating the NARMA10 dynamic system utilizing our photonic NG-RC chip. We use 1000 sampling factors for coaching and one other 1000 sampling factors for testing. Detailed information processing strategies for the NARMA10 process are supplied in Methodology. The experimental outcomes are proven in Fig. 4f–h. The NMSE is 0.107 utilizing solely 45 output nodes. The present finest experimental efficiency for this process in photonic RC with 50 nodes additionally studies an NMSE of 0.10721 however with a slower processing pace of 0.9 MHz, and a bigger bodily footprint because of the usage of a fiber-based system. Determine 4i highlights the superior efficiency of our system in each operation pace and NMSE for the NARMA10 process, in comparison with current bodily RC methods by way of experiments and simulations17,21,54,55,56,57,58.
Extending to WDM operation
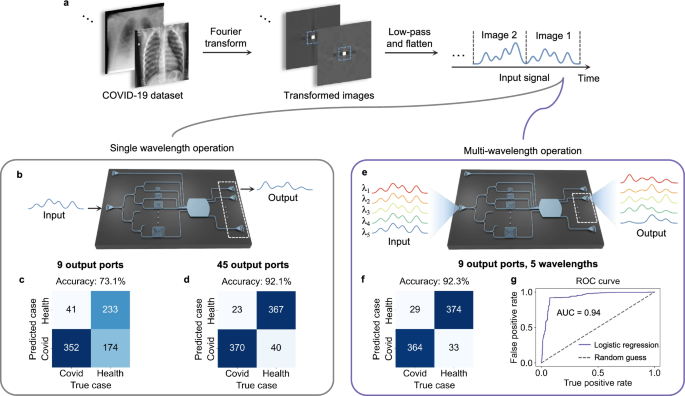
The carried out photonic NG-RC system will also be used for picture classification. Right here we exhibit a two-class COVID-19 classification process59. The dataset includes 2000 wholesome X-ray samples and 2000 COVID-19 samples and every pattern has 299 × 299 gray-scale pixels. We initially carry out picture preprocessing, together with Fourier rework and low-pass filtering, to lower enter dimensions, as proven in Fig. 5a. The Fourier rework may be thought to be a type of unitary matrix operation60. Due to this fact, these preprocessing steps may be completed utilizing photonic circuits61 or just an optical lens. The actual half values of the eight lowest spatial frequencies from the reworked pictures are flattened after which function inputs to our photonic NG-RC chip for coaching and testing. We use 3,200 picture samples because the coaching dataset, and 800 picture samples because the testing dataset.
a Picture preprocessing for COVID-19 process. b Experimental scheme utilizing a single wavelength. c Confusion matrix when utilizing a single wavelength and 9 output ports. d Confusion matrix when utilizing a single wavelength and 45 output ports. e Experimental scheme utilizing a number of wavelengths. f Confusion matrix when using WDM. g ROC curve when using WDM.
We first use a single wavelength because the service for demonstration. The enter sign is modulated onto a laser working at a wavelength of 1550 nm after which transmitted to the photonic NG-RC system for processing. Within the single wavelength case, just like earlier experiments, we gather output from 45 spatial output ports for information processing, as proven in Fig. 5b, and procure a classification accuracy of 92.1%, as proven in Fig. 5d, which is larger than these reported in refs. 59,62.
We then use a number of wavelengths to exhibit the scalability of our photonic NG-RC system enabled by WDM. On this experiment, 5 wavelengths (1548 nm, 1549 nm, 1550 nm, 1551 nm, and 1552 nm) are used to encode the identical enter sign. Because the alerts cross by way of the star coupler, every wavelength experiences a special switch perform matrix, leading to 5 distinct output alerts as proven in Fig. 5e. The variety of outputs determines the computational capability. When the wavelength quantity is P = 5 and the variety of the enter vector is N = 8, based on the operation precept, the required spatial output port is (frac{(N+1)(N+2)}{2P}=9).
As an instance the potential of utilizing WDM to increase computational capability, we gather information from solely 9 spatial output ports as an alternative of 45. If solely a single wavelength is used, the classification accuracy is diminished to 73.1% with the confusion matrix proven in Fig. 5c. Nevertheless, utilizing 5 wavelengths improves the accuracy to 92.3% with an space beneath the curve (AUC) of 0.94, corresponding to the case with a single wavelength however utilizing 45 output ports. Due to this fact, using WDM enhances the computing capability of our system and reduces the variety of required spatial output ports, thereby minimizing the system’s footprint and bettering scalability, particularly when the output port quantity is proscribed by optical SNR.
This articles is written by : Nermeen Nabil Khear Abdelmalak
All rights reserved to : USAGOLDMIES . www.usagoldmines.com
You can Enjoy surfing our website categories and read more content in many fields you may like .
Why USAGoldMines ?
USAGoldMines is a comprehensive website offering the latest in financial, crypto, and technical news. With specialized sections for each category, it provides readers with up-to-date market insights, investment trends, and technological advancements, making it a valuable resource for investors and enthusiasts in the fast-paced financial world.